Stability of Thin Shells

Overview

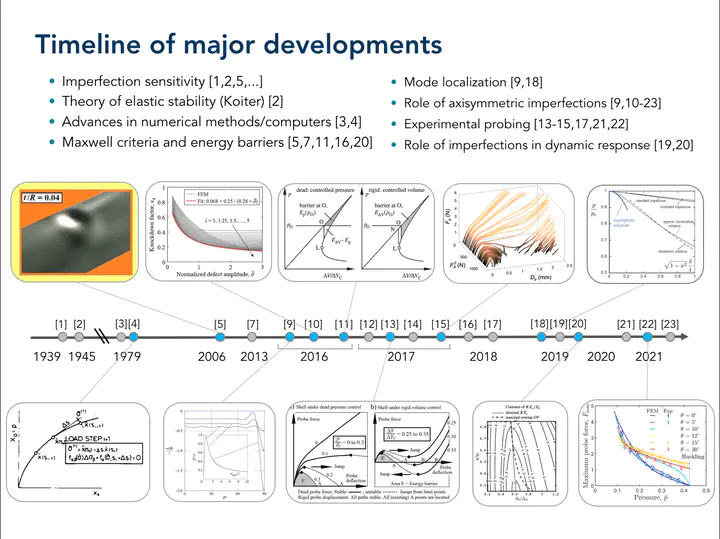
Recent advances in the understanding of stability in thin shells have been made by focusing on the localized nature of their post-bifurcation behavior, as opposed to historical efforts [W1] to rationalize the post-bifurcation response in terms of the classical global mode of Zoelly [W2]. In 2016, John Hutchinson elucidated how the classical global post-bifurcation mode of a spherical shell under uniform external pressure rapidly evolves into a stable, highly localized mode after bifurcation [W3]. He demonstrated that for realistically sized localized dimple-like imperfections $\delta$ of magnitude $\frac{\delta }{t}\ge 1$ the reduction in buckling strength from the classical prediction (termed the knockdown factor $\kappa$) plateaues to $\sim 0.2$. Following this work, these ideas were validated experimentally by Anna Lee and Pedro Reis [W4]. Quickly after, groups at Harvard, Cambridge, and MIT combined these developments with a refined understanding of the Maxwell load in the context of buckling [W5-W7] to subsequently develop methodologies for determining the knockdown factor in both cylindrical and spherical shells through non-destructive probing schemes [W7-W11]. Current efforts have successfully implemented these methods to map the stability landscape in cylindrical [W11, W12], spherical [W13, W14] and novel shell structures [W15], but the probing methods can only predict the correct knockdown factor by probing at the location of the largest imperfection. This leads naturally to my main interest within the stability of shells.

Question

Can we predict the knockdown factor $\kappa$ of a shell-structure associated with a localized imperfection without a priori knowledge of the defect location and/or geometry?

• [W1] Warner Koiter. “The nonlinear buckling behavior of a complete spherical shell under uniform external pressure, Parts I, II, III & IV”. Proc. Kon. Ned. Ak. Wet, 1969.
• [W2] Robert Zoelly. “Ueber ein Knickungsproblem an der Kugelschale”. PhD Thesis. 1915.
• [W3] John Hutchinson. “Buckling of spherical shells revisited”. In: Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, Nov 2016.
• [W4] Anna Lee et al. “The Geometric Role of Precisely Engineered Imperfections on the Critical Buckling Load of Spherical Elastic Shells”. In: Journal of Applied Mechanics, Aug. 2016.
• [W5] J. M. T. Thompson and G. H. M. van der Heijden. “Quantified ’shock sensitivity’ above the Maxwell load”. In: Int. J. Bifurcation & Chaos, 2013.
• [W6] Jiri Horak, Gabriel J. Lord, and Mark A. Peletier. “Cylinder Buckling: The Mountain Pass as an Organizing Center”, 2006.
• [W7] John Hutchinson and John Thompson. “Nonlinear Buckling Interaction for Spherical Shells Subject to Pressure and Probing Forces”. In: Journal of Applied Mechanics, June 2017.
• [W8] Joel Marthelot et al. “Buckling of a Pressurized Hemispherical Shell Subjected to a Probing Force”. In: Journal of Applied Mechanics, Sept. 2017.
• [W9] Emmanuel Virot et al. “Stability Landscape of Shell Buckling”. In: Physical Review Letters, Nov. 2017.
• [W10] John Hutchinson and John Thompson. “Imperfections and Energy Barriers in Shell Buckling”. In: IJSS, Jan. 2018.
• [W11] Simos Gerasimidis et al. “On Establishing Buckling Knockdowns for Imperfection-Sensitive Shell Structures”. In: Journal of Applied Mechanics, June 2018.
• [W12] Kshitij Yadav et al. “A Nondestructive Technique for the Evaluation of Thin Cylindrical Shells’ Axial Buckling Capacity”. In: Journal of Applied Mechanics, Jan. 2021.
• [W13] Arefeh Abbasi, Dong Yan, and Pedro Reis. “Probing the buckling of pressurized spherical shells”. In: Journal of the Mechanics and Physics of Solids, June 2021.
• [W14] Dong Yan et al. “Magneto-active elastic shells with tunable buckling strength”. In: Nature Communications, May 2021.
• [W15] Fabien Royer, John W. Hutchinson, and Sergio Pellegrino. “Probing the stability of thin- shell space structures under bending”. In: International Journal of Solids and Structures, 2022.